решите уравнение log1/2(x^2 -5x+6)=-1
Другие вопросы по теме Математика
Популярные вопросы
- Определите по карте координат точек 35° южной широты 59° западной долготы....
2 - 10 предложений на present simple с переводом...
1 - Как изменяются металлические свойства элементов в группах и периодах...
3 - Исследование продуктов на содержание крахмала название продукта обнаружен...
1 - Сочинение на тему я патриот и это ! нет идей...
1 - Тө мендегі жоспар негізінде мәтін құраңдар 1.до стық -қастерлі ұғым 2.д...
1 - «смысловой глагол to have» 9. who … “excellent” on history last semester?...
1 - Раздели сказку о мёртвой царевне и о семи богатырях на части. озаглавь...
2 - Почему к каждому падежу относится два падежных вопроса? именительный...
3 - Ученикам 4 класса предложили в субботу пойти на олимпиаду по , а в воскресенье...
3
Пошаговое объяснение:
ОДЗ: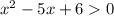
x ∈ (-∞;2) ∪ (3;+∞)