Решите уравнение касательной к графику функции

Другие вопросы по теме Математика
Популярные вопросы
- Нужен отзыв о книге в.железников чучело для читательского дневника. буду...
1 - 5кл. за три дня туристы км. в первый день они всего путиво второй день-20%...
1 - Развяжите уравнение: корень квадратный из х квадрат+ 3х-10+ корень квадратный...
3 - Два круга радиусов r и r внешне касаются. из центра одного круга проведена...
2 - Из точки а, лежащей на окружности, выходят одновременно два тела, движущиеся...
2 - Синквейн на тему нора (первое слово нора)...
2 - Во сколько раз отличаются сопротивления железной и алюминиевой проволки,...
3 - Закончите предложение: форму полутора числительное полтора имеет в падежах....
3 - Представить в виде многочлена(5a-3b) (4a-+b²)...
2 - Вычислите сколько граммов брома было в растворе, если при действии на него...
1
6
Пошаговое объяснение:
f(x)=x^3-4x+8x+6
f(0)=0^3-4*0+8*0+6=6
Пошаговое объяснение:
Пусть точка касания =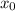 .
.
Тогда уравнение касательной имеет вид: