Решите уравнение и в ответе указать наибольший корень:
log_2^2(3x+5)+2log_2(3x+5)-3=0

-1

Пошаговое объяснение:

Область допустимых значений: 3x+5 > 0, x > -5/3

Введем замену: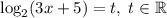 . Тогда t²+2t-3 = 0

По теореме Виета

Вернемся к замене:

Если t = -3, то

3x+5 = 2^(-3)

3x+5 = 1/8

24x+40 = 1

24x = -39

x = -39/24         (-39/24 > -40/24 = -5/3)

x = -13/8

________________

Если t = 1, то

3x+5 = 2¹

3x+5 = 2

3x = -3

x = -1                 (-1 = -3/3 > -5/3)

Оба найденных корня — -13/8 и -1 — входят в ОДЗ.