Решите уравнение и найдите корни этого уравнения на следующем промежутке
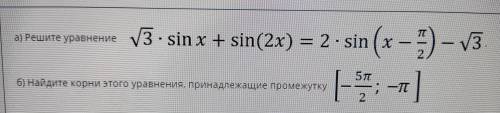
Другие вопросы по теме Математика
Популярные вопросы
- Вопытах было установлено, что модуль резины составляет 0,91 па. определите...
3 - Докажите, что уравнение sinx * sin ( п\2 - х ) = 1 не имеет корня...
2 - Вставьте глаголы do / have / spend в правильной форме. do shower every day?...
3 - Что такое сложное бессоюзное предложение?...
3 - Масса идеального газа равна m=10г. при t=1000k изохорически охлаждается...
2 - Написать сочинение на тема: моё хобби простыми словами, для начинающих....
2 - Придумайте предложения с причастием+наречием...
1 - Найдите значение выражения: arccos ( -1\2) + arcsin =2\2 - arctg (-1)...
3 - Купили конфеты трех видов. первого и второго видов вместе 20 кг, а второго...
3 - Найдите сумму всех целых значений числа k, при которых угол между векторами...
2
Корни уравнения, принадлежащие промежутку![[-\frac{5\pi}{2} ; -\pi ]](/tpl/images/2008/8879/ed1b1.png) :
: