Решите уравнение cosx-2sin2x*sinx-4cos2x-4sin^2x=0
Другие вопросы по теме Математика
Популярные вопросы
- Придумать 40 слов с непроизносимой согласной и с одним из слов составить предложениие...
1 - Для получения кислорода термическим разложением : а) перманганата калия kmno4;...
3 - Перевести на язык бірде т.өкеев: көксерек бойынша ғажайып фильм жасуға болады,-деп,...
2 - Встретил волк красную шапочку и спрашивает: сколько пирожков несёшь в корзинке,...
3 - Напишите сжатое все мы любим слушать музыку. вкусы и предпочтения, правда, у...
1 - Сколько литров водорода нужно для реакции с бромом, чтобы получилось 150л нbr?...
2 - Смежные углы относятся как 2: 7, найти больший угол....
2 - Какя масса вольфрама получится при взаимодействии 1.12 л водорода (н.у.) с оксидом...
2 - Реши пример: 2ц 2кг+3ц 99кг. а) 5ц 1001кг; б) 6ц 19кг; в) 6ц 1кг....
3 - Какое место в теории раскольникова занимает финансовая сторона преступления?...
3
Пошаговое объяснение:
Воспользуемся формулами двойного угла
1)
2)
Пусть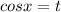 ,
, 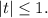
Условию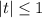 удовлетворяет
удовлетворяет 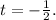
Значит