Решите уравнение Cos²x + Sinx + 1 = 0

Cos²x + Sinx + 1 = 0

Из основного тригонометрического тождества sin²x+cos²x= 1 выразим cos²x

cos²x= 1-sin²x

1 - sin²x + Sinx + 1 = 0 | : (-1)

sin²x - Sinx - 2 = 0

Пусть Sinx=t, тогда

t² - t - 2 = 0

D = (-1)² - 4*(-2) = 1+8 = 9 = 3²

Вернёмся к замене

В выражении Sin x = а есть условие, что |a|≤1 , что ещё можно выразить так -1≤a≤1

Получается первый корень нам не подходит и мы работаем только со вторым

Sin x = -1

, n∈Z

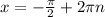ответ: , n∈Z