1. Математика
  2. Решите уравнение:3lg²x×10lgx+3=0​(письменно)

Решите уравнение:
3lg²x×10lgx+3=0​
(письменно)

Lordfantomchik Lordfantomchik    2   17.06.2020 02:25    0

Ответы
sebtetfGек5у sebtetfGек5у  15.10.2020 14:14

Решите уравнение:

3lg²x×10lgx+3=0​

применяем метод замены

lgx=t

3t^2+10t+3=0

D=b^2-4*a*c=10^2-4*3*3=100-36=64

t1=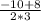\frac{-b+\sqrt{D} }{2*a}=\frac{-10+8}{2*3}=-2/6=-1/3

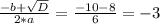
t2=\frac{-b+\sqrt{D} }{2*a} =\frac{-10-8}{6} =-3

делаем обратную замену

lgx=t

lgx=-1/3

x1=10^(-1/3)=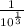\frac{1}{10^\frac{1}{3} }=\frac{1}{\sqrt[3]{10} }

lgx=-3

x2=10^(-3)=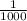\frac{1}{1000}

xПошаговое объяснение:

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
margo2200078 margo2200078  28.07.2019 22:30
12/14 * 1 1/3 + 6/7 найдите значение выражения...
Саша13398 Саша13398  28.07.2019 22:30
Из цифр 1, 3, 5 и 7 составьте все возможные двухзначные числа удовлетворяющие условиям: а) в разрядах десятков и единиц нет одинаковых цифр; б) в разрядах десятков и единиц могут...
meladse1105 meladse1105  28.07.2019 22:30
Запиши в порядке возрастания 9 кг, 980 г,9800г,8кг 900г...
kklll1g kklll1g  28.07.2019 22:30
Вырази в килограммах и граммах. 5007 г ,12120г,2 т 350 г,27ц18г. внимания! смотрите на запятые!...
MAXXB MAXXB  28.07.2019 22:30
Решите . а)сравните 30% от 60% и 60% от 30 б) сколько процентов составляет 30 от 40 в)найдите число 70% которого равны 21...
лариса219 лариса219  28.07.2019 22:30
Вцысткрне было 4800 л воды. 1 насос выкачал всю воду за 24 м а другой 40м за сколько минут можна выкачать всю воду если поставить2 насоса?...
kiryanova1969 kiryanova1969  28.07.2019 22:30
Вычислить: 15 км в кв.-20 га= 14 км 490 м : 18= 2 ч 5 мин -55 мин=...
DariaBlack777 DariaBlack777  28.07.2019 22:30
Мама ромы разрешила ему купить модельку автомобиля и плитку шоколада. сколькими рома может выбрать приз, если в магазине имеются 4 различные модельки автомобилей и 3 вида шоколадок?...
Помогите1411 Помогите1411  28.07.2019 22:30
Найдите отрицательный корень уравнения x2-x-6=0...
SaNur78 SaNur78  28.07.2019 22:30
Довжина прямокутныка 15см,площа якого 150см2 знайти периметр цього прямокутныка...

Популярные вопросы