Решите уравнение 3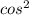 2x-sin2x+1=0
2x-sin2x+1=0
Другие вопросы по теме Математика
Популярные вопросы
- Если из суммы первых пятнадцати членов арифметической прогрессии вычитается...
1 - Одно из этих заданий... Заранее благодарю за ответ...
3 - 6. Распределите перечисленные вещества на три группы. Назовите эти...
1 - Основою піраміди є рівнобічна трапеція, основи якої дорівнюють 8 см...
2 - ответьте на эти вопросы дам 10 б прощу...
2 - быстр Напишите первоначальную формулировку периодического закона (1869г)...
1 - сколько будет стоить 609 брусники по цене 9373...
2 - При каких значениях параметра а система уравнений имеет нетривиальные...
3 - Найди наименьшее общее кратное чисел 220 и 165...
2 - Сколько национальностей проживают на территории Казахстана?...
2
Пошаговое объяснение:
нет корней, так как
n принадлежит Z.