Решите тригонометрическое уравнение.
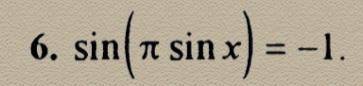
Другие вопросы по теме Математика
Популярные вопросы
- Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком...
3 - Из Москвы в Сергиев Посад в 8 ч. 33 мин. утра отправился экскурсионный...
1 - . Определите отрасль добывающей промышленности.1)транспортхимическая промышленность2)машиностроение3)добыча...
2 - НУЖНО СДАТЬ МНЕ ОЧЕНЬ В ТЕЧЕНИЕ 20 МИНУТ ОЧЕНЬ СДЕЛАТЬ ГЕОМЕТРИЮ РЕШЕНИЕ...
3 - Сколько точек пересечения имеют графики уравнений х-3у =16у -2х =3...
2 - 2). Жарық туралы берілген сөйлемдерді аяқтап жаз.Жарық түспейтін жерде...
3 - Номер 1440 математика реши сестемные уравнение подставки...
2 - Постройте график функций у =2-3x. С графика укажите значение функции,...
1 - Найди 2 одинаковых небесных тела и ответь, в честь чего назвали одну огромнуюю...
1 - Проанализируйте материал о развитие Японии в 19 веке и ответь на во почему...
1
sin(πsinx)=-1
πsinx=-π/2+2πк; кn∈Z;
sinx=-1/2+2к; к∈Z; IsinxI≤1. Поэтому
Подходит только 1)к=0; sinx=-1/2⇒х=(-1)ⁿarcsin(-1/2)+πn; n∈Z;
х=(-1)ⁿ ⁺¹π/6+πn; n∈Z;
к=0; sinx=-1/2⇒х=(-1)ⁿarcsin(-1/2)+πn; n∈Z;
х=(-1)ⁿ ⁺¹π/6+πn; n∈Z;