Решите то что на картинке и ответ желательно в таком же виде, с понятными символами.
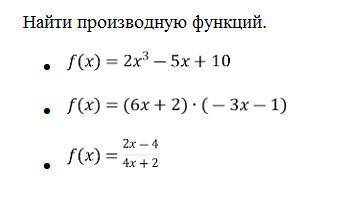
Другие вопросы по теме Математика
Популярные вопросы
- . Найдите глаголы в неопределённой форме. 1. рисуешь 4. готовлюсь...
2 - Напиши решение системы неравенств. (5(2-x) – 2(2x – 3) 2(3-х)2...
3 - Напишите сценарий к короткометражному хорору, который можно...
1 - Древнегреческих источниках саков называли скифами. 2. После...
1 - нарисовать картину с пейзажем перейдете по ссылке и там будет...
2 - Эссе на тему быть другом большая ответственность80 - 100 слов...
2 - Вставь пропущенные слова Духовенство относилось к …… сословию....
3 - Выполните действия дробями...
1 - Задание 1. Учебник стр.46 номер 813(1,3,5,7,9) 813. 1) 0,5 -...
3 - Вывод о питании одноклеточных водорослей (можно кратко) только...
2
Відповідь:
Покрокове пояснення:
Покрокове пояснення:
f'(x)=6x^2-5
f'(x)=6(-3x-1)-3(6x+2)=-18x-6-18x-6= -36x-12
f'(x)=((2х-4)/4х+2))'=(2×(4х+2)-4×(2х-4))/(4х+2)^2=(8х+4 -8х+16) / (4х+2)^2 = 20 / (4х+2)^2
1) 6x² - 5.
2) -36х - 12.
3) 5/(2x+1)².
Пошаговое объяснение:
1) f(x) = 2x³ - 5x + 10
f'(x) = (2x³ - 5x + 10)' = 2•3x² - 5 + 0 = 6x² - 5.
2) f(x) = (6x + 2)(- 3x - 1) = - 18x² - 6x - 6x - 2 = - 18x² - 12x - 2 ,
f'(x) = (- 18x² - 12x - 2)' = - 18•2x - 12 - 0 = -36х - 12.
3) f(x) = (2х - 4)/(4х+2) = 2•(х - 2)/(2•(2х+1)) = (х - 2)/(2х+1) .
f'(x) = ((х - 2)'•(2х+1) - (2х+1)'• (х - 2))/(2x+1)² = (2x+1 - 2•(x-2))/(2x+1)² = (2x + 1 - 2x +4)/(2x+1)² = 5/(2x+1)².