Решите , : сс 1)b\a-b: (a\a-b-a+b\a) 2)(a\a-b+a\b): a\a-b 3)(1\b2-1\a2)*ab\a+b(a2,а во 2 степени) 4)c-3\c-c2-9\c+3\c 5)b-2a\a-b*a2-b2\4a
Ответы
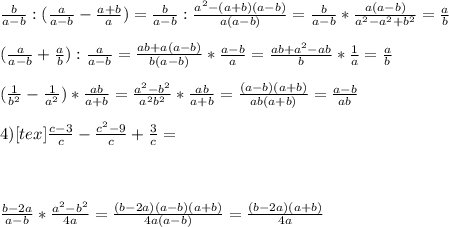 " alt="\frac{c-3}{c} - \frac{c^{2}-9 }{c} + \frac{3}{c}= \\ \\ \\ \\ \frac{b-2a}{a-b} * \frac{ a^{2}- b^{2} }{4a}= \frac{(b-2a)(a-b)(a+b)}{4a(a-b)}= \frac{(b-2a)(a+b)}{4a}" /> " />
" alt="\frac{c-3}{c} - \frac{c^{2}-9 }{c} + \frac{3}{c}= \\ \\ \\ \\ \frac{b-2a}{a-b} * \frac{ a^{2}- b^{2} }{4a}= \frac{(b-2a)(a-b)(a+b)}{4a(a-b)}= \frac{(b-2a)(a+b)}{4a}" /> " />
Другие вопросы по теме Математика
Популярные вопросы
- Напишіть мініесей на тему: «Королівство Руське та його роль в...
3 - Что больше 13/11 или 13/8,...
3 - ответить на вопросы на 67стр, см текст (64-65-66) По немецки...
1 - 354 вправа української мови 9 клас Караман...
1 - Open the brackets The earth (1. know) (2. revolve) around the...
2 - Посмотрел: рукав новенького фрака был весь испорчен. Сделать...
1 - У чым бачыцца тыповасць сатырычных вобразау п есы зацюканы апостал...
3 - Характиристика Тома Сойєра на Українській 15рядків...
2 - КАРАУЛЛЛ МЕГААА Подайте у вигляді нескінченого десяткового дробу...
3 - Упражнение 3. Полностью разорившись (1) отправился он в Петербург...
3