Решите систему уравнений.
Принимается любой метод.
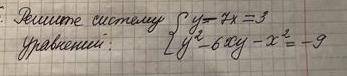
Другие вопросы по теме Математика
Популярные вопросы
- Укажи подчинительное словосочетание со связью СОГЛАСОВАНИЕ: 1) что-нибудь...
2 - 17esirde hansi materikler hele kesf olunmamisdi?...
2 - придумай преддложение: подлежащее,сказуемое,дополнение,определениеДОМ...
2 - Якими природоохороними документами в Україні регулюеться питання...
1 - Марічка придбала зошит, іграшку та цукерки і заплатила за все 61...
1 - Електричний нагрівник доводить до кипіння воду, взяту при температурі...
1 - Log(0,5) 0,5 * log(3) 1/81 - 7^log(7) 2...
3 - 7 класс, зарубежная литература «Чи вдалося Айзеку Азімову зобразити...
2 - ABC AB BC AC Найдите са свае, если L1= 120° -2= 40°...
3 - Длина прямоугольника 9 см, а ширина на 3 см Чему равен периметр...
2
Решим данную систему методом подстановки: в верхнем уравнении можно выразить переменную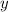 через
через  .
.
Решим нижнее уравнение отдельно:
По теореме Виета:
Вернёмся к исходной системе.
И в итоге получаем две пары решений:
ответ: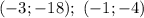 .
.
ответ на прикреплённом файле