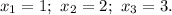Решите систему методом гаусса
5x₁-x₂-x₃=0
x₁+2x₂+3x₃=14
4x₁+3x₂+2x₃=16
Другие вопросы по теме Математика
Популярные вопросы
- Сложите целые части десятичных дробей 3,99 и 12,56...
1 - Отметьте правильный вариант продолжения фразы 1)человек разумный появился а)1,5...
1 - Запишите в виде десятичной дроби а) 4/11 б) -2 6/25 в) 32/45...
2 - Масса ящика с яблоками 12 кг, а масса пустого ящика в 6 раз меньше. сколько кг....
1 - Составьте предложения с прямой речью на схемы: п, -а, - п , а: п! -а...
1 - Ккакой части речи относится слово в...
3 - Вставьте пропущенные буквы,запишите проверочные слова.в проверяемых словах выделите...
1 - Может ли быть целым числом значение выражения 1) 1/х. 2)x/x+1...
2 - Фонетический разбор слов мечта, ельник, еловые....
2 - Объединяет клеточные структуры в единое целое, является местом протекания реакций...
2
Запишем расширенную матрицу системы и приведем ее к треугольному виду при элементарных преобразований матрицы, которые выполняются над строками:
Ранг матрицы: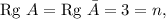 где
где 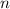 - число неизвестных.
- число неизвестных.
Система совместимая, значит, имеет единственное решение.
Ставим в соответствие расширенной матрице систему, эквивалентную выходной, решение которой совершаем снизу вверх:
ответ: