Решите пример.
ответ нужен с решением.
tgx=tg5x
Другие вопросы по теме Математика
Популярные вопросы
- Опишите,какими вы видите героев-панфиловцев.почему об их подвиге поется в гимне...
3 - 75 ! метапредметная работа по языку и для 7 класса 1 вариант часть 1 тестовые...
3 - Сгрядки собрали 72 морковки часть морковки израсходовали а другую часть связали...
3 - 1. какое количество вещества оксида серы (iv) so2 содержит 30 *1023 молекул?...
1 - Составить текст 5-6 предложений на тему осень используя языковые средства...
3 - Заполнить таблицу. 6 класс батыево нашествие на русь дата : направление : итоги...
3 - Если ионы щелочных металлов не окрашены, как объяснить окраску паров этих элементов...
3 - Какие полезные ископаемые добывают в астрпханской области?...
1 - 55 , . необходимо составить графическую формулу: mnoh(clo4)2...
3 - Гнилое морфологические признаки подскажите...
2
Перенесем все в одну часть:
Представим тангенсы как отношение синуса к косинусу:
Приведем к общему знаменателю:
Заметим в числителе формулу синуса разности:
Дробь равна нулю, когда числитель равен нулю, а знаменателе нулю не равен:
Найдем, при каких х числитель равен нулю:
Найдем при каких х знаменатель обращается в ноль:
Заметим, что вторая серия "посторонних корней"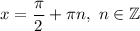 входит в решение
входит в решение  . Значит, их необходимо исключить из решения.
. Значит, их необходимо исключить из решения.
Представив первую серию "посторонних корней" в виде , понимаем, что других посторонних корней в решении
, понимаем, что других посторонних корней в решении  нет.
нет.
Таким образом, среди серии корней , обращающих в ноль числитель, встречаются корни
, обращающих в ноль числитель, встречаются корни 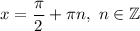 , обращающие в ноль знаменатель. Значит, это посторонние корни, и их необходимо исключить из решения.
, обращающие в ноль знаменатель. Значит, это посторонние корни, и их необходимо исключить из решения.
Итоговый ответ: