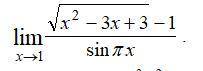
Другие вопросы по теме Математика
Ника85527
20.08.2019 15:20
petrachenkov201
20.08.2019 15:20
sstresseddoutt
20.08.2019 15:20
Иван7962
20.08.2019 15:20
6Evgeny11111
20.08.2019 15:20
romanovanelya
20.08.2019 15:20
валера200331
20.08.2019 15:20
StarAl73
20.08.2019 15:20
Популярные вопросы
- Визначте зайве слово великий , церква святого андрія , чудь , литва...
3 - дайте ответ класс история Казахстана....
2 - 5 клас,зарубіжна література,продовження повісті Поліанна та Том Соєр...
2 - Запишите пропущенное слово ___ как черта массовой культуры стала одной...
1 - Периметр прямоугольника равен 12 см. Длину одной из сторон прямо-...
3 - Соотнеси термин и его определение...
2 - розкажіть основні зміни про системи української освіти у 1920-1930...
1 - мне... те кто знает географию очень надо......
2 - Бұйрықты сөйлемді қатыстырып, тақырыпқа сай диалог құрастыру...
2 - Какие идеи Д,И,Фонвизина могут быть близки молодому поколению сегодня?...
1
ответ: 0 .
Пошаговое объяснение:
. . . = lim [ √(x² - 3x + 3 ) - 1 ]/(πx) = lim [ √(x² - 3x + 3 ) - 1 ]* [ √(x² - 3x + 3 ) + 1 ]/(πx ) X
x-->0 x-->0
X [ √(x² - 3x + 3 ) + 1 ] = lim( x² - 3x + 3 - 1 )/(πx ) * [ √(x² - 3x + 3 ) + 1 ] =
x-->0
= lim( x² - 3x + 2 )/(πx ) * [ √(x² - 3x + 3 ) + 1 ] = 0/(π * 1 ) = 0 .
x-->0