Решите определенный интеграл
Очень нужно
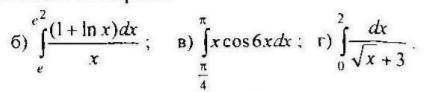
Другие вопросы по теме Математика
Популярные вопросы
- Определить свойства горных пород гранита и известняка результаты...
2 - Составить 3 предложения со словами грустный, ясный, опасный...
2 - Написать сочинение по ! на тему : what can you say for and against...
3 - Определите характер оксид азота (ii). a) кислотный в) основный...
2 - Еки жалан,еки жайылма сойлем керек.....
2 - Сила 20н растягивает пружину динамометра на 5 см. какова цена...
1 - Умиши было a конфет. 3/8 своих конфет он съел. сколько конфет...
3 - Where do you usually celebrate your birthday? -перевести...
2 - Дан треугольник abc , сторона aв=корень из 17 , вс=4см , а ас=5см....
1 - Выражение: а) 2 квадратный корень из 5 минус квадратный корень...
1
б
в
По частям:
г