Решите номер 7 и 8. укажите решение
Другие вопросы по теме Математика
Популярные вопросы
- 79-сабақ Дауылдан қорықтым1. Кестені толтыр. Теңізбен байланысты сөздерді...
2 - Історія україни 7 клас гісем §12. план 2-6 розвиток русі...
2 - На каких основных принципах базировалась внешняя политика США после Второй...
3 - Один из Штатов в Северной Америке 6 букв...
1 - Найдите корочень уравнения 8x-(6-x)=7x-9...
2 - У листопаді 6 днів світило сонце, 12 днів ішов дощ, 9 днів було пасмурно,...
2 - Слова объяснениеСловарь зовёт......
1 - Практическая работа «Описание одной из стран Северной или Западной Африки»...
1 - Қазақстандағы өзендер мен көлдер эссе ...
1 - Синтаксистік талдау жассап беріңіздерші өтініш >...
1
7.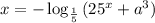
Пусть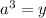 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию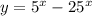 :
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно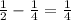 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,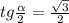
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем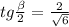
ответ: 4 : 3