Решите неравенство:  написать не только решение, но и максимально понятное объяснение !
написать не только решение, но и максимально понятное объяснение !
Другие вопросы по теме Математика
Популярные вопросы
- 1)-2 1/6 + 3 1/15=2)-4 7/9 + 5/6=3)5 2/7 + (3 7/8)=...
1 - Сопоставь ситуацию с соответствующим решением. Почти всю неделю...
3 - объясните тему реакции ионного обмена 9 класс химия своими словами...
3 - Гомологом 2-метилпентена-1 является: А) бутандиен-1,3 Б) метилпропен...
3 - Задание 1-го уровня сложности. Заполните таблицу 17. Таблица 17Функции...
3 - Известно, что а в квадрате + b в квадрате + с в квадрате =17 и а-b-с=5....
1 - 7. Складіть рівняння кола радіуса 10, яке проходить через точку...
2 - Расстояние между двумя посёлками пешеход за 6 ч, а велосипедист...
2 - 310, 11редставьте наиде неправильно обновенной дроби смешанные чела:2)...
3 - Выполните сложение 9 +(-1целая...
3
Чтобы было нагляднее, вычтем из всех частей этого неравенства :
:
Выражение не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел
не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел  и
и 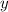 выполняется одно и только одно из соотношений:
выполняется одно и только одно из соотношений: 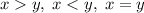 ), поэтому оно может равняться только нулю:
), поэтому оно может равняться только нулю:
В мат. анализе с приведения к подобному неравенству (только для функций) доказывается существование первого замечательного предела - "теорема о двух конвоирах (миллиционерах)"
Решение простое. х ≥ а², когда х либо больше, либо равно а².
Другая часть неравенства х ≤ а², когда х либо меньше, либо равно а².
Пересечение решений, т.е. их общее решение х=а² и будет ответом. а²≤а²≤а², т.е. при х=а² выполняется как одна часть неравенства, так и другая, поэтому х=а²
ответ х=а²