1. Математика
  2. Решите неравенство log|x-2|(3-|x|)

Решите неравенство log|x-2|(3-|x|)< =1

Yaroslav1640 Yaroslav1640    2   08.05.2019 23:39    0

Ответы
89261774454 89261774454  09.06.2020 17:55

x \in (-3;-0.5]\cup (1;2)\cup (2;2.5]

Пошаговое объяснение:

log_{ |x - 2| }(3 - |x| ) \leqslant 1 \\ ( |x - 2| - 1)(3 - |x| - |x - 2| ) \leqslant 0 \\ (x - 3)(x - 1)(x + 0.5)(x - 2.5) \geqslant 0

и используя метод интервалов + ОДЗ получим ответ.

Пояснения:

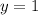1) 3- |x|-|x-2| : график "корыто", ветви вниз, тангенс наклона по модулю равен 2, основание y=1, абсциссы точек углов 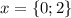x=\{0; 2\}, поэтому пересечения Ox при 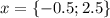x = \{-0.5;2.5\}, поэтому: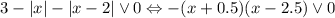3-|x|-|x-2|\vee 0 \Leftrightarrow -(x+0.5)(x-2.5)\vee 0

2) ОДЗ:

\left\{\begin{matrix}|x-2|0\\ |x-2|\neq 1\\ 3-|x|0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x -3\\ x \neq 1\\ x \neq 2\\ x < 3\end{matrix}\right. \Leftrightarrow x\in (-3;1)\cup (1;2)\cup (2;3)

3) Метод интервалов: см. прикрепленный файл


Решите неравенство log|x-2|(3-|x|)< =1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
St1ler St1ler  10.10.2021 20:04
Найдите наибольшее натуральное число n, при котором n^100 5^150...
LORDytGucci LORDytGucci  10.10.2021 20:05
Длина прямоугольника 65 см а его ширина в пять раз меньше Чему равна площадь прямоугольника...
TamerlanKalken TamerlanKalken  10.10.2021 20:06
Составьте и решите упражнение по типу задачи 66, используя сведения о вашем класса...
Викусик1258 Викусик1258  10.10.2021 20:09
Укажите квадратное уравнение сумма корней которого равна - 12 а произведение корней равно...
nastja2011i nastja2011i  10.10.2021 20:09
Сравните: 5 — и 0,7 7 , с объяснением...
Finikotik Finikotik  10.10.2021 20:10
Памагите с 7 сверху правила к нему...
Шамшербек Шамшербек  10.10.2021 20:10
Упростить выражение.sin(a) \cos( - b ) - \sin(a - b)...
ZaykaYmnik ZaykaYmnik  10.10.2021 20:10
6x+6y4xy-4ay8a-2в8х+6у11х-4х14х²+хх⁷+х⁸6n²-10nd...
olenapolova4 olenapolova4  10.10.2021 20:13
Решить задачи расписать точно: 9. При делении 102 на загаданное число получается такой же результат, как при делении числа 408 на число, которое больше загаданного...
Ятот Ятот  10.10.2021 20:13
Какие числа одновременно кратные 2,5,10 являются решением неравенства? 89 c 110...

Популярные вопросы