Решите неравенство (2-3x)*log2x-1(x^2-2x+2) заранее огромное (50б)
Другие вопросы по теме Математика
Популярные вопросы
- Решите задание по химии, нужно сделать таблицу( )...
2 - 1 0 2 пишет стихи.• Люди каких профессий имеют отношение к искусству?•...
2 - решить задачу.у першому раундi компютерноi гри Олеся набрала 24000 очок,а...
2 - ДО 21:00 4. Назовите причины, вызывающие выветривание горных пород? 5....
3 - Казахский язык 4класс подпишусь...
1 - Жазылым. Кестені толықтыр. (распредели слова по столбикам) Армандайды,...
3 - Снежная королева, владычица над зимой и смертью, Ледяная Дева, Фея Льдов,...
2 - Списать, вставить пропущенные буквы. Найди имена числительные. Обозначь...
2 - У чотирикутнику ABCD кути A і B прямі, AB=20 см, BC=30 см, AD=50 см (див....
3 - 4. Өлеңді көшіріп жаз. Барқыт тау, жасыл дала, зеңгір* аспан.зеңгірКүміс...
2
ОДЗ:
1) 2x - 1 > 0; 2x > 1; x > 0,5
2) 2x - 1 ≠ 1; 2x ≠ 2; x ≠ 1
3) x² - 2x + 2 > 0; ⇔ (x² - 2x + 1) + 1 > 0;
(x - 1)² + 1 > 0 - выполняется при любых значениях х.
ОДЗ : x ∈ (0,5; 1) ∪ (1; +∞)
Метод интервалов с учётом ОДЗ
(0,5) ----------- [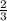 ] ++++++++++ (1) ------------>x
] ++++++++++ (1) ------------>x
ответ: x ∈ (0,5;2/3] ∪ (1; +∞)