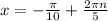Решите на множестве R уравнение: В теме синусы и косинусы и т.д
Оно на фотографии ниже
Решите полным ответом и если возможно то в письменном виде ответ тоесть в тетради, ну или как вам легче
Заранее ,

Другие вопросы по теме Математика
Популярные вопросы
- Капитан Нұрхан Досұлының қылмыскерді құрықтауыЭссе...
2 - Составить 5-7 примеров с глаголами hatte,war...
1 - Тест по познанию мира по теме «Гуины» Usparul .1.Кто такие гунны?А) кочевой...
2 - 5.143. Представьте в виде произведения:1) x8+x4+1;2) х4+x=y2+у;...
3 - Напишите сочинение на тему Над чем рассказ Леского Человек на часах заставил...
3 - Обозначение рек на карте относится к виду условных знаков...
3 - Лии язык для него СліПота? Докажитеэто язык родного8 Работа в группах.12ражена...
1 - При короткому замиканні гальванічного елемента з ЕРС 1,8В одержується...
2 - Можно эссе на тему *Одежда красит человека*...
2 - 7 вопросов по теме организация ввода и вывода данных...
1
Эти уравнения не такие страшные и сложные, какими могут показаться на первый взгляд, здесь всего-навсего нужно делать замены:
а)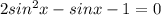
Пусть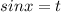 , имеем:
, имеем:
Вернёмся к замене:
Теперь найденные корни подставляем вместо t в sinx = t и ищем новые корни:
ответ: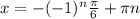 и
и 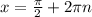
б)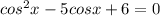
Пусть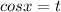 , имеем:
, имеем:
Вернёмся к замене:
Мы знаем, что cos x не может быть больше 1 или меньше -1 (область значений: [-1; 1]), поэтому данное уравнение не имеет корней:
x ∈ ∅
Аналогичная ситуация:
x ∈ ∅
ответ: корней нету (или x ∈ ∅, или х ∉ R)
в)
Пусть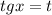 , имеем:
, имеем:
Вернёмся к замене:
Обрати внимание на то, что тангенс может быть каким угодно числом (его область значений (-∞; +∞)), поэтому это уравнение имеет корни:
ответ: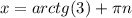 и
и 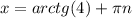
г)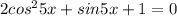
Всю малину портит косинус, поэтому сделать замену тут нельзя. Чтобы решить эту проблему, добудем синус из косинуса по формуле: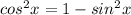
Имеем:
Пусть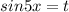 , имеем:
, имеем:
Второй корень не подходит, т.к.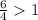 .
.
Вернёмся к замене:
ответ: