Решите логарифмическое неравенство
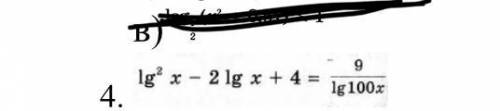
Другие вопросы по теме Математика
Популярные вопросы
- Формой научного познания, дающей целостное отображение существенных...
3 - Согласно модели Большого Взрыва, на раннем этапе эволюции Вселенная...
2 - Единицы измерения различных систем: связаны между собой не связаны...
1 - Систематизирующий фактор, который был взят за основу Д.И. Менделеевым...
2 - Статистические методы не дают однозначных и полностью достоверных...
1 - Метатеторетический уровень характерен только для наиболее продвинутых...
1 - Оптические явления связаны с проявлением _ взаимодействия электромагнитного...
3 - Уровней научного познания существует: два четыре три пять...
2 - Для познания наиболее надежными и удобными являются динамические...
3 - Естествознание работает с более грубыми измерениями и явлениями,...
1
ОДЗ: х>0
пусть lgx = t, lgx не равен -2.
ответ: 10