Решите , используя формулы родной вероятности и байеса:
на склад от трех поставщиков поступило 200, 300 и 500 изделий соответственно. продукция первого поставщика имеет 5% брака, второго – 6%, третьего – 4%. найдите вероятность получения со склада годного изделия.
Другие вопросы по теме Математика
Популярные вопросы
- Используя одну процедуру, построить фигуру...
3 - К прудине динамометра повесили груз. Воспользовавшись рисунком определите...
1 - Определите преобладающий ветер...
2 - Дополни пословицу в ученье трудно,да плоды......
2 - Кестені толтырыңыз қазақстан тарихы...
1 - 1(Прочитайте выразительно фрагмент поэмы Александра Сергеевича Пушкина Медный...
2 - БЕЖИН ЛУГ легкий тест Задание 6 Кто придет к людям в день солнечного затмения?...
2 - Составить кластер Капитанская дочка ...
2 - ГЕОГРАФИЯ - 8 В ПРИРОДНЫЕ ЗОНЫ И ВЫСОТНЫЕ ПОЯСАУРОКВИДЕОКОНФЕРЕНЦИЯОткрыть...
3 - 7. В основании большей части материка находится: а) платформа б) древние складчатые...
2
Пусть событие А - изделие окажется бракованным и рассмотрим гипотезы :
Из условия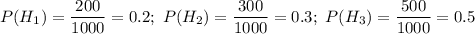 и условные вероятности
и условные вероятности
По формуле полной вероятности, вероятность получения со склада бракованного изделия равна
Тогда вероятность получения со склада годного изделия равна
ответ: 0,952.