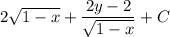Решите интеграл: ((x+y-2)/(1-x)^(3/2))dx
y - как константа
Можно как можно подробнее мат. анализа не изучали
Другие вопросы по теме Математика
Популярные вопросы
- Будь ласка до ть написати твір на 6 речень на тему мій улюблений інструмент...
1 - Речення на німецькій мові зі словом kartoffelpuree...
1 - Sinx+sin3x=0до ть, терміново ...
2 - Не отривая ручку от бумаги перечеркни все 9 точок 4 ровними линиями...
3 - (С ЛИНЕЙКИ И КАРАНДАША, 1. Начертите два перпендикулярных отрезка, которые:а)...
3 - Самостоятельная работа Передвижение воды и питательных веществ в растении...
2 - векторы 9 класс в №1(а,б,в,г,) ,в. № 2(а,б)...
1 - Ракета масою 4т летить зі швидкістю 0,5км/с Від неї відокремлюється частина...
2 - Первые предположения о шарообразности Земли были выдвинуты в А) Древнем...
2 - Какое отношение выдумка имеет к горным добытчикам? Из сказа Бажова Медной...
1
Использованные свойства неопределенных интегралов:
Использованные формулы:
ответ: