Решите и объясните .
подпишите к какой 22 или 23 вы написали решение.
зарание .

Ответы

online19 29.07.2020 07:23

22. Пусть a — первая цифра числа, все его остальные цифры — A, n — количество цифр в числе. Тогда

$\overline{aA}=5\overline{A}\\10^{n-1}a+A=5A\\10^{n-1}a=4A\\A=\frac{10^{n-1}}{4}a=2^{n-3}*5^{n-1}a=25*10^{n-3}a$

При n ≥ 5 у числа A на конце будет как минимум 2 нуля на конце (идёт умножение какого-то числа на 100, 1000 и т. д.), а значит, и у числа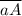 $\overline{aA}$ тоже будет не менее двух нулей на конце, что невозможно по условию.

При n = 4 исходное число состоит из 4 цифр, значит число A состоит из 3 цифр.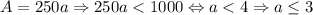 $A=250a \Rightarrow 250a$

Чем больше первая цифра, тем больше само число. Пусть a = 3, тогда A = 250 * 3 = 750. Искомое число: 3750. Действительно, 3750 : 5 = 750.

ответ: 3750

ПОКАЗАТЬ ОТВЕТЫ

vladsmolin4554 29.07.2020 07:23

23.

Логично, что для того, чтобы результат дроби был наибольшим числитель должен быть наибольшим из возможных, а знаменатель наименьшим.Так как в знаменателе чисто произведение, можно сразу сказать, что С*Р*А*З*У это произведение чисел от 1 до 5. Теперь вопрос, в каком порядке умножать числа? Представим числитель в виде:

Р*А*З+Р*Е*З*А*И=Р*А*З*(1+Е*И)

так как Е и И не входят в знаменатель можем смело повесить на них 8 и 9

а на Р*А*З 3,4,5 и без разницы в каком порядке(смена мест множителей результат не изменит)

Получаем:

$\displaystyle\frac{3*4*5+3*8*5*4*9}{1*3*4*5*2}=36,5$