1. Математика
  2. Решите два предела, с

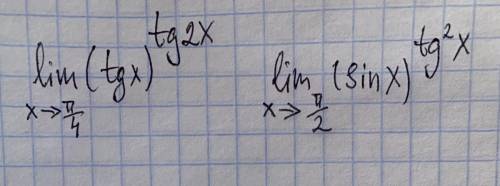
Решите два предела, с замены, без использования правила Лопиталя заранее


Решите два предела, с замены, без использования правила Лопиталя заранее

Dilyash2007 Dilyash2007    1   23.08.2020 11:59    1

Ответы
ппво ппво  15.10.2020 16:10

x-\frac{\pi }{4}=t

x=t+\frac{\pi }{4}

x\rightarrow \frac{\pi}{4} ;t\rightarrow 0

tgx=tg(t+\frac{\pi}{4})

tg2x=tg2(t+\frac{\pi}{4})=tg(2t+\frac{\pi}{2})=-ctg2t

Обозначим:

a=\lim_{t \to 0} tg(t+\frac{\pi}{4})^{-ctg2t}

Логарифмируем:

lna=ln\lim_{t \to 0} tg(t+\frac{\pi}{4})^{-ctg2t}

Знак предела и знак непрерывной функции можно менять местами:

lna=\lim_{t \to 0} lntg(t+\frac{\pi}{4})^{-ctg2t}

Применяем свойство логарифма степени

lna=\lim_{t \to 0}(-ctg2x)\cdot lntg(t+\frac{\pi}{4})

Запишем в виде дроби:

lna=-\lim_{t \to 0}\frac{ lntg(t+\frac{\pi}{4})}{tg2t}=-\lim_{t \to 0}\frac{2t lntg(t+\frac{\pi}{4})}{(tg2t)2t}=- \lim_{t \to 0}\frac{2t}{tg2t}\cdot\lim_{t \to 0} \frac{ln tg (t+\frac{\pi}{4})}{2t} =\\\\=-1\cdot \lim_{t \to 0} \frac{ln tg (t+\frac{\pi}{4})}{2t} =

неопределенность (0\0)= ( проще по правилу Лопиталя):

\lim_{t \to 0} \frac{ln tg (t+\frac{\pi}{4})}{2t} = \lim_{t \to 0}\frac{\frac{1}{tg(t+\frac{\pi}{4})\cdot cos^2(t+\frac{\pi}{4} ) } }{2} =-\frac{1}{4}

lna=\lim_{t \to 0} lntg(t+\frac{\pi}{4})^{-ctg2t}=-\frac{1}{4}

Значит,

a=\lim_{t \to 0} tg(t+\frac{\pi}{4})^{-ctg2t}=e^{-\frac{1}{4}}=\frac{1}{\sqrt[4]{e}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Garri14 Garri14  19.08.2019 00:10
Выполните действие: 130*62-66649: 83+601...
Jenya19885 Jenya19885  19.08.2019 00:10
Решить : из 20метров ткани пошили 50 наволочек . сколько наволочек можно пошить из 10 метров ткани ? нужно сегодня )...
arinka3859 arinka3859  19.08.2019 00:10
Первый автомобиль выехал из города со скоростью 50 км/ч,а второй выехал на полчаса позже и двигался со скоростью 60км/ч....
k666goblin k666goblin  19.08.2019 00:10
Округлите 31285634 до десятков , до сотен , до тысяч , до сто тысяч , до миллионов ....
666777зпа 666777зпа  19.08.2019 00:10
Напишите условие заранее . скорость утки равна 96 километров чат, а скорость чайки 48 километров час. во сколько раз больше скорость утки, чем скорость чайки? насколько километров...
ladavasilenko ladavasilenko  19.08.2019 00:10
Решить ? павел десяток орешков купил. восемь орешков купил михаил. встретили свету и в спешке поровну всем поделили орешки. семьдесят восемь копеек при этом за фундучки заплатила...
beynyadima beynyadima  19.08.2019 00:10
Постройте ломаную линию состоящую из двух отрезков 4 см 5 см и 6см 9мм вычислите её длину...
Dimasik3310 Dimasik3310  19.08.2019 00:10
Черепашке найти родственные слова-зима,зимний,зимой,зиму,зимующий,зимовать....
mamonova86 mamonova86  19.08.2019 00:10
Экзотические животные самая главная информация...
muratov20011 muratov20011  19.08.2019 00:10
Как зависит площадь квадрата от длины его стороны?...

Популярные вопросы