Решите дифференциальные уравнения с разделяющимися переменными.
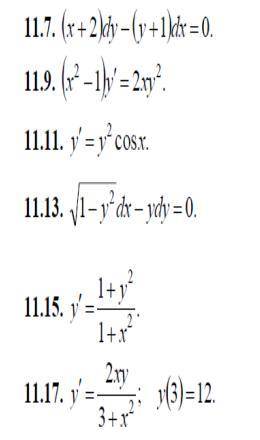
Другие вопросы по теме Математика
Популярные вопросы
- Осуществите цепочку превращений: ca —- h2 —- hcl —- zncl2...
3 - Вреестр обьектов нематериального культурного наследия народов югры включена технология,связанная...
3 - Напишите сообщение про валентина афанасьевича обручева про его исследования...
3 - Спишите, вставляя буквы и расставляя пропущенные знаки препинания. графически...
3 - На шапочку и шарф требуется одинаковое количество шерсти и 1 кг 50 г шерсти бабушка...
2 - Выписать из рассказа золотой петух 20 слов с приставками....
2 - 7метров 16миллиметров сколько будет в миллиметрах...
2 - Как изменится скорость реакции, температурный коэффициент которой 2, при повышении...
1 - 1)чему равно давление на рельсы восьмиколёсного вагона массой 60000 кг, если...
1 - Много пропустил назовите в.ва: ch (3)-ch-ch3-ch-ch3-ch3...
3
Пошаговое объяснение:
Уравнения с разделяющимися переменными
Пусть в выражении f(x,y)=f1(x)f2(y), то есть уравнение может быть представлено в виде y'=f1(x)f2(y) или в эквивалентной форме:
M1(x)M2(y)dx + N1(x)N2(y)dy = 0.
Эти уравнения называются дифференциальными уравнениями с разделяющимися переменными.
Если f2≠0 для , то, с учетом того, что y'=dy/dx, получаем откуда, с учетом инвариантности дифференциала первого порядка, имеем .
Аналогично, для уравнения во второй форме, если получаем или, интегрируя обе части по x, .
НАЗНАЧЕНИЕ СЕРВИСА. Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений с разделяющимися переменными.
x*y*dx + (x+1)*dy
=
0
Решить
ПРИМЕР 1. Для дифференциального уравнения y' = ex+y имеем y' = exey, откуда e-ydy = exdx или, интегрируя обе части по x, e-y = ex + C и, наконец, y = -ln(-ex + C).
ПРИМЕР 2. Решить уравнение xydx + (x+1)dy = 0. В предположении, что получаем или, интегрируя, lny = -x + ln(x+1) + lnC, отсюда y = C(x+1)e-x. Решение y = 0 получается при C = 0, а решение x = 1 не содержится в нем. Таким образом, решение уравнения y = C(x+1)e-x,