1. Математика
  2. Решите дифференциальное

Решите дифференциальное уравнение с разделяющимися переменными: xyy'=x^2+y^2

Кица234 Кица234    1   12.07.2019 23:00    0

Ответы
frankinshtein228 frankinshtein228  03.10.2020 02:13
Линейное однородное дифференциальное уравнение 1-го порядка.
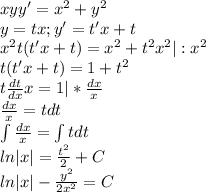
xyy'=x^2+y^2\\y=tx;y'=t'x+t\\x^2t(t'x+t)=x^2+t^2x^2|:x^2\\t(t'x+t)=1+t^2\\t\frac{dt}{dx}x=1|*\frac{dx}{x}\\\frac{dx}{x}=tdt\\\int\frac{dx}{x}=\int tdt\\ln|x|=\frac{t^2}{2}+C\\ln|x|-\frac{y^2}{2x^2}=C
ПОКАЗАТЬ ОТВЕТЫ
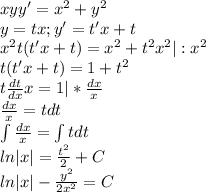
Другие вопросы по теме Математика
Маrprokap Маrprokap  26.11.2020 19:05
решить задания, обведеное с лева. Буду очень благодарен ​...
hyyeblan5577 hyyeblan5577  26.11.2020 19:05
Сколько листов в формате А3 получится из одного листа формата А И ещё напишмте как вы определили, тем самым я дальше будут решать такие примеры на подобии! ​...
sasha11751 sasha11751  26.11.2020 19:05
Маша живёт в квартире № 70. В её доме 6 этажей, по 4 квартиры на каждом этаже. В каком подъезде и на каком этаже живёт Маша?...
Емаилком002 Емаилком002  26.11.2020 19:05
Определи вид треугольника две стороны которого равны 8.см и 12 см. а пиримтр -- 28см.​...
сэрго2002 сэрго2002  26.11.2020 19:05
Укажите одночлен наибольшей степени: а) -8,5а^9b^8 b) 2,5x^2y^2z^9 c) 10 1/2a^3b^12c d) 1,25a^12b^6 e) 18,2a^10b^2 Решите...
gsajhja gsajhja  26.11.2020 19:05
Можете мне у меня проста пустая голава​...
vovan8881 vovan8881  26.11.2020 19:04
Подберите вместо букв цифры так чтобы получилось верное равенство (одинаковыми буквами обазначены одинаковые цыфры, разными буквами- разные) ТУ=Р×Н=И+Р ответи очень нужно​...
dog126 dog126  26.11.2020 19:04
два поезда шли навстречу один ехал 50 км ч другой 60 км ч через через 3 часа они встретились Найди расстояние между городами​...
Gianfed Gianfed  26.11.2020 19:04
Задание No5. Решите уравнениеа)15+х=3124.21 ​...
Anna111864 Anna111864  26.11.2020 19:04
найдите произвонные функций...

Популярные вопросы