Решите : дальность l полета снаряда выпущенного с начальной скоростью v0 из орудия, наклоненного по углом φ к горизонту, определяется формулой: l=(vо^2sin2φ)/g где g=9.8 м/сек2 найти угол, при котором дальность полета снаряда будет наибольшей.
Другие вопросы по теме Математика
Популярные вопросы
- Составьте характеристику отрасли мирового хозяйства по плану (на выбор 1 отрасль:...
2 - Знайдіть площу рівнобедреного трикутника, бічна сторона якого дорівнює 17см,...
3 - ВСЁ КРОМЕ ЗАДАНИЯ С АУДИО >...
2 - Вірш англійською про англію. ів...
3 - В XIX веке отменили крепостное право. Как изменилась жизнь крестьян? Приведи...
2 - Жазылым.Айтылым. 2-тапсырма. Семантикалық картаны толтыр. Түсіндіріп айт.(Заполните...
3 - Духовне життя мешканців причорномор я...
2 - по братский заранее огромное кто сделает ...
2 - Полный текст Повесть Кладовая солнца...
1 - Скласти ланцюжок почуттів у ліричного героя у вірші „Чому, сказати, я й сам...
2
Для ответа на этот вопрос нужно взять пройзводную по углу:
Для определения максимума нужно приравнять производную к нулю
Данное выражение может быть равно нулю, если значение косинуса равно нулю, а это возможно если угол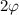 составляет 90 градусов. Значит угол
составляет 90 градусов. Значит угол 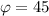
Если же исходное выражение выглядело:
То по аналогии:
tex]\frac{v_{0}^{2}}{g}Sin(2\varphi)=0[/tex]
Тогда получается, что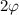 составляет 0 или 180 градусов. Значит угол
составляет 0 или 180 градусов. Значит угол 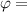 0 или 90
0 или 90