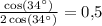решите (cos26-cos86)/2cos34
Другие вопросы по теме Математика
Популярные вопросы
- Запиши числа: 9 сотен тысяч 6 тысяч 3 сотни 1 единица. 3 десятка...
3 - Вклассе 15 девочек и 14 мальчиков. на 8 марта каждый из мальчиков...
3 - Движение является равноускоренным, если выполняется закономерность:...
2 - Ещё раз найдите натуральные числа а и б,не делявшиеся друг на...
2 - Подобрать 2 загадки с глаголами 1 и 2 спряжения...
2 - Вдвух мешках по 50 кг сахара. после того как из одного мешка...
2 - Переведите , надо diese stadt ist eine uralte metropole von...
3 - 1.каждый день по дороге в школу тебе встречается пожилой мужчина,...
2 - У2 и 3 группа крови,определите их генотип,если у них родилось...
3 - Встолбик 22•33,64•24,42•68,37•66,63•36,65•1000,1500•100,100•380,2900•10...
1
используем формулу "разность косинусов":
тогда числитель =
числитель
используем формулу привидения:
тогда числитель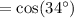
Исходное выражение =