1. Математика
  2. Решите что сможете, проф математика

Решите что сможете, проф математика у меня, а сдаю обычную, химбио


Решите что сможете, проф математика у меня, а сдаю обычную, химбио

anya377 anya377    3   16.10.2020 08:26    0

Ответы
brenczan brenczan  15.11.2020 08:27

Пошаговое объяснение:

Номер 1. 90<α<180, cos(α)=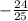-\frac{24}{25}

Ограничения на угол α накладывают ограничения на sin(α): sin(α) >0 , т.к. угол находится во второй четверти.

sin^2(\alpha )+cos^2(\alpha)=1\\sin(\alpha)=\sqrt{1-cos^2(\alpha)}\\ sin(\alpha)=\sqrt{1-\frac{24^2}{25^2} }=\frac{7}{25} \\ tg(\alpha)=\frac{sin(\alpha)}{cos(\alpha)} =-\frac{7}{24}\\ ctg(\alpha)=-\frac{24}{7}

Номер 2.

а) cos(3π/5)*tg(π/9)

Сравним каждый множитель с 0:

tg(π/9)>0 т.к. sin(π/9)>0 и cos(π/9) >0, и если делить положительное число на положительное, то получится положительное

cos(3π/5) : 3π/5 - тупой угол => его косинус отрицательный

Мы умножаем положительное число на отрицательное и получаем отрицательное => cos(3π/5)*tg(π/9)<0

б)sin(4)cos(5)

Аналогично:

sin(4): π<4<2π=> sin(4)<0

cos(5): 3π/2<5<5π/2 =>cos(5)>0

sin(4)cos(5)<0

Номер 5.

8sin^2(\alpha )-5cos^2(\alpha)=7\\cos^2(\alpha)=1-sin^2(\alpha)\\8sin^2(\alpha)-5(1-sin^2(\alpha))=7\\8sin^2(\alpha)-5+5sin^2(\alpha)=7\\13sin^2(\alpha)=12\\sin^2(\alpha)=\frac{12}{13}\\ cos^2(\alpha)=\frac{1}{13}\\ tg^2(\alpha)=\frac{sin^2(\alpha)}{cos^2(\alpha)}=12

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
gagikgrigoryan gagikgrigoryan  09.07.2019 20:30
Впарке разбили две клумбы прямоугольной и квадратной формы.у клумбы прямоугольной формы длина составляет 6 м, а ширина 4м. у клумбы квадратной формы сторона 5 м. площадь...
iloveyou27 iloveyou27  09.07.2019 20:30
На прямой отмечено 20 точек так что расстояние между любыми соседними точками было одно и то же.найдите это расстояние между крайними точками равно 760 см...
Alexandra335 Alexandra335  09.07.2019 20:30
Вынесите за скобки наибольший общий делитель коэффициентов: 1) 12а+20b 2)16c+24d 3)30m+42n 4)48x+60y 5)18a+45b 6)18c+63d 7)49m+21n 8)15m+25n...
mikhalyukmahem mikhalyukmahem  09.07.2019 20:30
Зал освещают 8 люстр по 9 лампочек на каждой и ещё 10 лампочек над сценой сколько всего лампочек освещают этот зал измени вопрос 2) чтобы она решалась так 9*8-10=62(л.)...
dianavoronina4545 dianavoronina4545  09.07.2019 20:30
Было 4 яблоки осталось 3 сколько всего останется яблок...
Slysly Slysly  09.07.2019 20:30
Кновому году мама купила елочные украшения на сумму 560 рублей оказалось что елочные бусы дороже набора елочных шаров в 3 раза сколько стоит каждое украшение в отдельности?...
yan551029 yan551029  09.07.2019 20:30
Сумма двух чисел 246 , а разница 32. найдите эти числа...
anuta1244 anuta1244  09.07.2019 20:30
Поле заселяли за три дня . 1день-засеяли 1/6 поля 2 день -засеяли 3/8 поля 3день-? какая часть всего поля была засеяна в 3 день?...
nastiia4 nastiia4  09.07.2019 20:30
Записать комплимент маме или учителю....
alisa2847274 alisa2847274  09.07.2019 20:30
Сколько тетрадных клеток занимает 12см...

Популярные вопросы