Решите, 30 !
-5x^2 + 8x-5 меньше 0
докажите, что при любом значении х верно неравенство:

Question

Математика: Решите, 30 ! -5x^2 + 8x-5 меньше 0 докажите, что при любом значении х верно неравенство:

danilsmetanov6 · Answer

Есть функция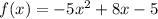 f(x)=-5x^2+8x-5

Если надо доказать, что она лежит ниже оси OX при любых х, то для начала надо найти её нули. Для этого нужен дискриминант. Если он отрицателен, то корней нет, то есть этих самых нулей нет. При этом коэффициент при старшей степени равен -5, соответственно, при D<0 график действительно будет лежать ниже оси OX.

Найдем теперь этот самый дискриминант:

Здесь b - четное число, найдем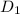 D_1

Напомню, что

$$D_1=\bigg(\frac{b}{2}\bigg)^2-a\cdot c$

$-5x^2+8x-5=0; D_1=4^2-(-5)\cdot (-5)=16-25=-9$

Можно и D посчитать

$D=b^2-4\cdot a\cdot c=8^2-4\cdot(-5)\cdot (-5)=64-100=-36$

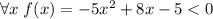D<0, -5<0 ⇒ $\forall x \; f(x)=-5x^2+8x-5$ (вообще этот символ не пиши, напиши "для любого х" вместо него, это квантор всеобщности, просто для ознакомления, если будет интересно, почитаешь)

Решите, 30 ! -5x^2 + 8x-5 меньше 0 докажите, что при любом значении х верно неравенство:

Популярные вопросы

Решите, 30 !
-5x^2 + 8x-5 меньше 0
докажите, что при любом значении х верно неравенство: