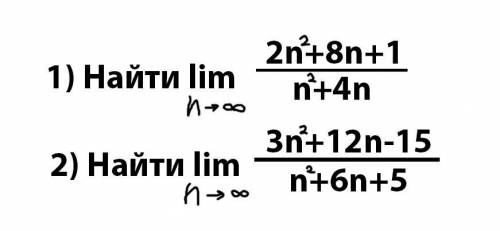
Математика: решить, желатьельно как можно быстрее

решить, желатьельно как можно быстрее

Ответы

издательство1 07.01.2021 03:33

$2; \quad 3;$

Пошаговое объяснение:

$1) \quad \lim_{n \to \infty} \frac{2n^{2}+8n+1}{n^{2}+4n};$

Имеем неопределённость типа

$\frac{\infty}{\infty};$

Воспользуемся методом Лопиталя. Для этого найдём производную числителя и знаменателя:

$\lim_{n \to \infty} \frac{(2n^{2}+8n+1)'}{(n^{2}+4n)'}= \lim_{n \to \infty} \frac{4n+8}{2n+4}= \lim_{n \to \infty} \frac{2(2n+4)}{2n+4}=2;$

$2) \quad \lim_{n \to \infty} \frac{3n^{2}+12n-15}{n^{2}+6n+5};$

Имеем неопределённость типа

$\frac{\infty}{\infty};$

Решаем аналогично предыдущему примеру:

$\lim_{n \to \infty} \frac{(3n^{2}+12n-15)'}{(n^{2}+6n+5)'}= \lim_{n \to \infty} \frac{6n+12}{2n+6}= \lim_{n \to \infty} \frac{(6n+12)'}{(2n+6)'}= \lim_{n \to \infty} \frac{6}{2}=3;$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Lala0911 19.04.2021 15:34

3 Составь выражения: а) У Мальвины было п сольдо. Она купила се-бе платье за а сольдо и 4 ленты по b сольдо.Сколько денег осталось у Мальвины?б) Кот Леопольд купил мышaтaм...

exhedzo 19.04.2021 15:33

Решите задачи , если что то не понятно пишите ...

kashamovasha 19.04.2021 15:33

Выразите в метрах и запишите в виде десятичных долю ей: 1)18 см. 2) 27 дм. 3) 86 дм 2 см. 4) 6 см. 5) 18 см...

Malvina1903 19.04.2021 15:33

Состав и реши задачи по таблице...

kmodeste 19.04.2021 15:33

длина аллеи 540 м. От 2 концов аллее побежали одновременно навстречу друг другу Петя его собака пират. через 2 минуты Петя и пират встретились. с какой скоростью бежал Петя,...

lera956 19.04.2021 15:33

683. Двома автомобілями пер шим автомобілем перевезли 20 т, а другимрету. Скількирейсів зробив кожен автомобіль, якщо їхня вантажність о-накова, а загальна кількість рейсів...

catxripunowa 19.04.2021 15:33

9+10+23+89+12-10-3 сколько будет?...

ева211078 19.04.2021 15:33

Решите столбиком 1 508. 214 :(48 000 - 47 884)...

kuanyshbek2003 19.04.2021 15:33

Амалдарды орндаңдар матемтика ...

vasilisa12234 19.04.2021 15:33

Позначте на координатній площині точки К-1; —1) і М(2;- 4). Проведіть відрізок КМ. Знайдіть коорди- нати точки перетину відрізка КМ з віссю кординат. Решите !❤️...

решить, желатьельно как можно быстрее

Популярные вопросы