решить
Запишите комплексное число в стандартной тригометрической форме
-4-3i

Ответы

МаТеМаТиК200411 23.08.2020 17:28

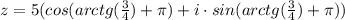
ответ: $z=5(cos(arctg(\frac{3}{4})+\pi)+i\cdot sin(arctg(\frac{3}{4})+\pi))\\$

Пошаговое объяснение:

$|z|= \sqrt{4^2+3^2}=5\\$

Поскольку x < 0, y < 0, то arg(z) находим как:

$arg(z)=\phi=\pi + artcg(\frac{|Im(z)|}{|Re(z)|})\\\phi=\pi + artcg(\frac{|-3|}{|-4|})=arctg(\frac{3}{4})+\pi\\$

Следовательно тригонометрическая форма:

$z=5(cos(arctg(\frac{3}{4})+\pi)+i\cdot sin(arctg(\frac{3}{4})+\pi))\\$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

yanakuzmina1 13.01.2021 16:29

Реши уравнение и опредили его корень прям...

vikap888 13.01.2021 16:28

Найдите числовое значение выражения a×c, если...

akabakova56gmailcom 13.01.2021 16:28

№677(7-9),№680 математика 5 класс...

elena090107 13.01.2021 16:28

Aru212 13.01.2021 16:28

temur4 13.01.2021 16:28

Antik3006 13.01.2021 16:28

Найти коэффициент при x^12 в разложении (x^5-x-e^2)^20...

sinan1922abdullaev 13.01.2021 16:27

Закончи запись. 6,5ц=...цкг...

mrsexobeat308 13.01.2021 16:27

олеся14111 13.01.2021 16:27

|5|=-5 правильно скажите паже ...

решить Запишите комплексное число в стандартной тригометрической форме -4-3i​