Решить задания с дифференциацильными уравнениями очень нужно разобраться!

Ответы

Psix73 17.01.2022 08:10

$Y=\lfloor X\rfloor\sim Geom(1-e^{-\lambda}); EY=\dfrac{1}{e^{\lambda}-1}$

Пошаговое объяснение:

С учетом определения целой части числа, имеем

$P(Y=k)=P(\lfloor X\rfloor=k)=P(k\leq X$

Заметим, что

$P(k+1\leq X|k\leq X)=\dfrac{P(k+1\leq X,k\leq X)}{P(k\leq X)}=[\{k+1\leq X\}\Rightarrow\{k\leq X\}]=\dfrac{P(k+1\leq X)}{P(k\leq X)}=\dfrac{1-P(X$

[К слову, можно доказать и более общую формулу, которая соответствует свойству под названием "отсутствие памяти"]

Возвращаемся к исходным расчетам:

$(*)=e^{-\lambda k}\cdot (1-e^{-\lambda})=(e^{-\lambda })^k\cdot (1-e^{-\lambda})$

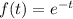Т.к. по определению $\lambda 0$ , функция $f(t)=e^{-t}$ неотрицательна и монотонно убывает на , причем f(0)=1 , то $e^{-\lambda}\in[0;1]$ . Но тогда и $1-e^{-\lambda}\in[0;1]$ .

Отсюда, нетрудно заметить, наше распределение есть не что иное, как геометрическое распределение с параметром $p=1-e^{-\lambda}$ .

Значит, матожидание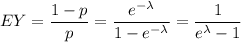 $EY=\dfrac{1-p}{p}=\dfrac{e^{-\lambda}}{1-e^{-\lambda}}=\dfrac{1}{e^{\lambda}-1}$ .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

дариииинннкккааа 23.04.2020 14:44

Площадь осевого сечения цилиндра равна 3, а высота цилиндра равна 1,5. Найти площадь полной поверхности...

Lilit66696 23.04.2020 14:44

ответь (не производя построения), в каком координатном угле расположена точка M(−1;13)....

qwerty1352 23.04.2020 14:44

Решайте уравнение 19,6-4у=12,5 5х-2х=8,7 3у+у+9,52=10,4...

Polinakovta 23.04.2020 14:43

Мама отримала премію. Частину витратла на харчі,а п яту частину на кіно. Залишилось 105 гривень.Яку премію мама отримала....

sherilblo 23.04.2020 14:43

7×7×7= 10×10= 8×8×8= 4×4= 9×9×9= 20×20=...

Iejsjsjsj 23.04.2020 14:43

Собрали 24 кг клюквы а голубики в 3 раза меньше, на сколько меньше собрали голубики , чем клюквы?...

Anna11111199933445 23.04.2020 14:43

Масса угля в железнодорожном вагоне 60 т. Самосвал может взять третью часть этого груза.сколько рейсов надо сделать на самосвале,чтобы разгрузить 6 таких вагонов?;краткая запись,...

radif01 01.03.2021 19:27

Сколько будет стоить килограм сушеных яблок если отвентить гайку от паровоза?...

кирилл5775065421423 01.03.2021 19:27

Число сперва увеличили на 20%, а потом уменьшили на 15%. Увеличилось или уменьшилось число?На сколько процентов?...

TriPPPix 01.03.2021 19:27

Теңдеулерді шеш.174 : x = 900 - 897125.3+= 525і трај патот- топ...

Решить задания с дифференциацильными уравнениями очень нужно разобраться!

Популярные вопросы