решить задачу. Методом итераций решить систему линейных уравнений с точностью до 0.001 предварительно оценив число необходимых для этого шагов.
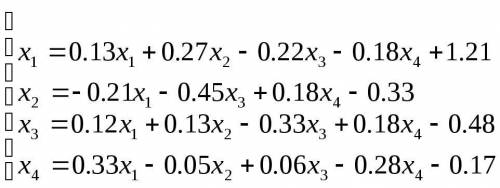
Другие вопросы по теме Математика
Популярные вопросы
- По графику зависимости путей от времени двух тел I и II, движущихся равномерно, определи скорость...
1 - Периметр р/б треугольника равен 4,9 м. Его основание больше боковой стороны...
3 - Введение понятие о германе генри гесс...
1 - Пройденый путь при равномерным движение,это а.время движения поделить на скоростьб.время...
1 - 10 ) Если угол между векторами острый, то скалярное произведение а) положительное...
2 - Составить программу вычисления значения функции , для любого а, введенного...
3 - Докажи, что четырёхугольник ABCD является прямоугольником, найди его площадь,...
1 - 1) Fill in the missing word: fussy, packed, pinch 1. I really don t know what...
1 - Танец его значение в жизни человека ...
2 - Рассчитайте сколько влаги сконденсируется во влажном подвале размерами 6м...
1
Для начала, преобразуем уравнения данной системы в вид, пригодный для итераций. В нашем случае это будет вид x = f(x), где x - вектор неизвестных.
Заданная система уравнений имеет вид:
1) 2x1 - x2 + x3 = 1
2) x1 + 3x2 - 2x3 = -2
3) -x1 - 4x2 + 5x3 = 0
Преобразуем каждое уравнение таким образом, чтобы x был выражен через остальные переменные:
1) x1 = (1 + x2 - x3)/2
2) x2 = (-2 - x1 + 2x3)/3
3) x3 = (5x1 + 4x2)/(-5)
Таким образом, система уравнений примет вид:
1) x1 = (1 + x2 - x3)/2
2) x2 = (-2 - x1 + 2x3)/3
3) x3 = (5(1 + x2 - x3)/2 + 4(-2 - x1 + 2x3)/3)/(-5)
Теперь приступим к самим итерациям. Пусть x(0) - начальное приближение, и на каждом шаге n будем вычислять новое значение x(n) по следующей формуле:
x(n) = f(x(n-1)) = (1 + x2(n-1) - x3(n-1))/2
x(n) = (-2 - x1(n-1) + 2x3(n-1))/3
x(n) = (5(1 + x2(n-1) - x3(n-1))/2 + 4(-2 - x1(n-1) + 2x3(n-1))/3)/(-5)
Выберем начальное приближение, например, x(0) = (0, 0, 0).
Теперь будем последовательно подставлять значения x(n-1) в формулы, пока не достигнем требуемой точности 0.001. В каждом шаге будем проверять точность по формуле:
| x(n) - x(n-1) | < 0.001
Продолжаем итерации до тех пор, пока не выполнится условие точности.
Будем продолжать итерации в следующем шаге, пока условие точности не выполнится. После выполнения условия точности, получим приближенное решение системы линейных уравнений с требуемой точностью.
Надеюсь, я смог объяснить вам процесс решения данной задачи. Если у вас возникнут еще вопросы, обязательно задавайте!