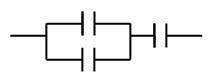
решить задачу к экзамену по дисциплине "Надёжность и диагностика вычислительных устройств и систем" Задача:Известны: λ - интенсивность отказов конденсаторов; λ0, λ3= λ1- интенсивность отказов конденсатора соответственно по отрыву и замыканию (пробою); φ0= λ0/( λ0+ λ1) – вероятность того, что возникший отказ конденсатора произойдет из-за обрыва; t – время непрерывной работы схемы. Предполагается, что последействие отказов отсутствует. Найти вероятность безотказной работы схемы соединения конденсаторов, показанной на рис. 1

Для решения данной задачи нам потребуется вычислить вероятность безотказной работы каждого параллельно соединенного элемента и затем найти произведение этих вероятностей.

Для начала, возьмем параллельно соединенные элементы A и B. Вероятность безотказной работы элемента A обозначим как P(A), а вероятность безотказной работы элемента B - P(B).

Из условия задачи мы знаем, что интенсивность отказов конденсатора по отрыву равна λ0, интенсивность отказов конденсатора по замыканию (пробою) равна λ1, а общая интенсивность отказов конденсатора равна λ (λ = λ0 + λ1).

Теперь рассмотрим элемент A. Так как отказ конденсатора произойдет из-за обрыва с вероятностью φ0 = λ0 / (λ0 + λ1), то вероятность безотказной работы элемента A равна 1 - φ0.

Аналогично, вероятность безотказной работы элемента B равна 1 - φ1, где φ1 = λ3 / (λ3 + λ1).

Теперь мы можем найти вероятность безотказной работы параллельного соединения элементов A и B. Обозначим эту вероятность как P(A∩B).

P(A∩B) = P(A) * P(B)

Так как элементы A и B соединены параллельно, то при наличии только одного отказа из обоих элементов, вероятность безотказной работы параллельного соединения будет равна произведению вероятностей безотказной работы каждого элемента.

Таким образом, вероятность безотказной работы параллельного соединения элементов A и B равна:

P(A∩B) = (1 - φ0) * (1 - φ1)

Теперь рассмотрим параллельное соединение полученного параллельного соединения элементов A и B с элементом C. Обозначим вероятность безотказной работы полученного соединения как P(A∩B∩C).

Аналогично, вероятность безотказной работы элемента C равна 1 - φ3, где φ3 = λ3 / (λ3 + λ1).

Тогда вероятность безотказной работы параллельного соединения элементов A∩B и C равна:

P(A∩B∩C) = P(A∩B) * P(C)

P(A∩B∩C) = (1 - φ0) * (1 - φ1) * (1 - φ3)

Вероятность безотказной работы всей схемы соединения конденсаторов, показанной на рисунке, равна вероятности безотказной работы параллельного соединения элементов A∩B∩C.

Необходимо учесть, что данный рассчет предполагает отсутствие последействия отказов. В реальности может быть необходимо учитывать возможность последствий отказов.

Надеюсь, эта пошаговая инструкция поможет вам понять и решить данную задачу. Если у вас возникнут дополнительные вопросы, пожалуйста, обратитесь за помощью!