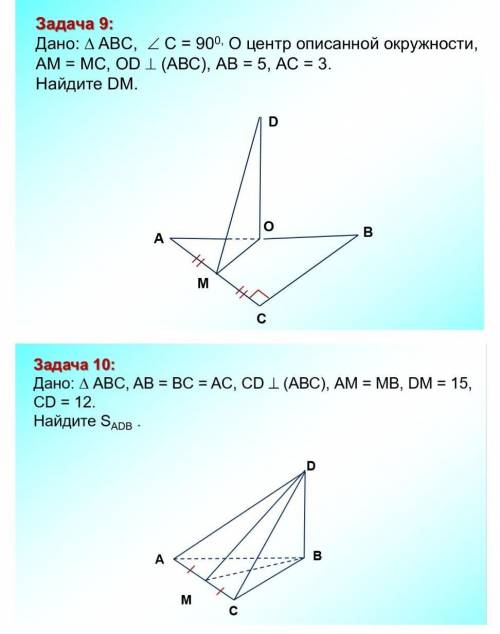
Решить задачи по геометрии

Добрый день! Я рад, что вы обратились со своим вопросом. Посмотрим на задачу и попробуем ее решить.

У нас даны две окружности, одна вписана в другую. Задача состоит в том, чтобы найти площадь кольца, образованного между этими окружностями.

Шаг 1: Найдем радиусы обеих окружностей. Мы знаем, что большая окружность вписана в квадрат, сторона которого равна 8 см. Раз мы знаем сторону квадрата, мы можем найти диагональ квадрата, применяя теорему Пифагора.

Диагональ квадрата равна √(сторона^2 + сторона^2) = √(8^2 + 8^2) = √(64 + 64) = √128 = 8√2 см.

Так как диагональ квадрата равна диаметру большой окружности, то радиус большой окружности будет равен половине диаметра, то есть равен 8√2 / 2 = 4√2 см.

Шаг 2: Теперь найдем радиус маленькой окружности. Мы знаем, что маленькая окружность касается сторон квадрата, а также большей окружности. Так как большая окружность касается стороны квадрата, то расстояние от центра этой окружности до стороны квадрата равно ее радиусу.

Радиус маленькой окружности будет равен радиусу большой окружности минус расстоянию от центра этой окружности до стороны квадрата.

Расстояние от центра этой окружности до стороны квадрата равно половине диагонали квадрата. Так как мы уже рассчитывали диагональ квадрата на предыдущем шаге (8√2 см), то расстояние будет равно 8√2 / 2 = 4√2 см.

Теперь можем найти радиус маленькой окружности: 4√2 см - 4√2 см = 0 см.

Шаг 3: Найдем площадь кольца, образованного между этими окружностями.

Площадь кольца можно найти вычитанием площади маленькой окружности из площади большей окружности.

Площадь большей окружности равна π * (радиус большой окружности)^2 = π * (4√2)^2 = 16π * 2 = 32π см^2.

Площадь маленькой окружности равна π * (радиус маленькой окружности)^2 = π * (0)^2 = 0π = 0 см^2.

Площадь кольца будет равна 32π - 0 = 32π см^2.

Ответ: Площадь кольца, образованного между окружностями, равна 32π см^2.

Надеюсь, что мое объяснение было понятным и полезным. Если у вас остались вопросы, пожалуйста, не стесняйтесь задавать их мне.