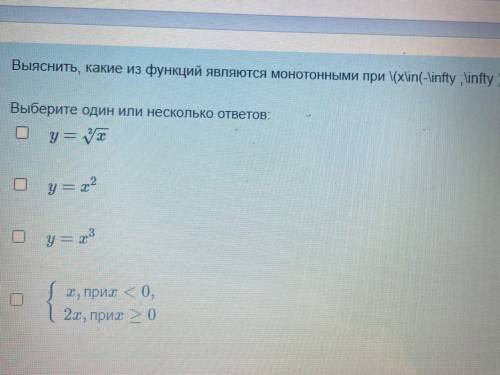
решить Выяснить, какие из функций являются монотонными
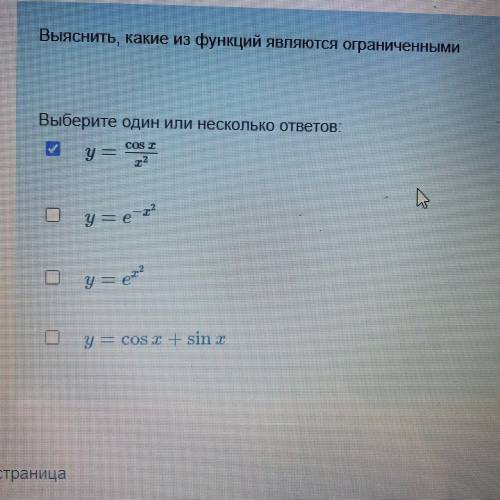
Выяснить, какие из функций являются ограниченными

Добрый день!

Для начала давайте разберемся, что значит быть монотонной функцией. Монотонная функция это такая функция, у которой значения возрастают или убывают в зависимости от изменения аргумента.

Для определения монотонности функций мы воспользуемся графиками функций, которые даны на картинках.

Первая картинка представляет собой графики нескольких функций. Давайте рассмотрим каждую функцию по отдельности и определим, является ли она монотонной.

1. Функция A: Мы видим, что при увеличении значения аргумента, значения функции также увеличиваются. Значит, она является монотонно возрастающей.
2. Функция B: В данном случае, при увеличении значения аргумента, значения функции убывают. Это означает, что функция B - монотонно убывающая.
3. Функция C: Здесь мы видим, что при увеличении значения аргумента, значения функции то увеличиваются, то убывают. Мы не можем назвать ее монотонной, так как нет строгой зависимости между значениями аргумента и значениями функции.
4. Функция D: При увеличении значения аргумента, значения функции то убывают, то увеличиваются. И снова, нет строгой зависимости, поэтому функция D не является монотонной.

Теперь перейдем ко вторым картинкам. На этих графиках функции представлены в виде таблиц. Для определения монотонности функций, будем анализировать значения функций при увеличении значения аргумента.

1. Функция E: При увеличении значения аргумента, значения функции увеличиваются. Она монотонно возрастает.
2. Функция F: Значения функции при увеличении аргумента сначала увеличиваются, а затем убывают. Это означает, что функция F не является монотонной.

Теперь перейдем к определению ограниченности функций. Ограниченная функция - это функция, значения которой лежат в некотором заданном диапазоне.

Обратимся к первым картинкам:

1. Функция A: Видим, что значения функции на графике ограничены сверху и неограничены снизу. То есть, функция A является сверху ограниченной.
2. Функция B: Здесь значения функции ограничены и сверху, и снизу. Функция B - ограниченная.
3. Функция C: На графике видно, что значения функции не ограничены сверху и снизу, т.е. функция C - неограниченная.
4. Функция D: Здесь значения функции ограничены сверху и неограничены снизу. Функция D является ограниченной сверху.

Перейдем к вторым картинкам:

1. Функция E: Значения функции на графике не ограничены сверху и неограничены снизу, поэтому функция E - неограниченная.
2. Функция F: Значения функции на графике ограничены снизу, но неограничены сверху. Таким образом, функция F является ограниченной снизу.

Надеюсь, ответ был полным и понятным. Если у тебя возникнут еще вопросы, не стесняйся задавать!