решить все задания решить все задания.">
Другие вопросы по теме Математика
Популярные вопросы
- Напишите реакции темновой и световой фаз фотосинтеза...
3 - Сравните число 75% которого равно 40,с числом 40 % которого равно 75...
3 - 22 как можно проверять согласные в корнях имен прилагательных, глаголов?...
1 - Почему тарас бульба убил своего сына остапа?...
2 - Вырази в метрах, децтметрах и сантиметрах: 875 см, 743см, 506см, 310см,...
3 - Написать статью о человеке которым я восхищаюсь и сочинение о моем любимом...
2 - Найдите корни уравнения x²+7x-60=0; y²-10y-24=0; m²+m-90=0; 3t²+7t+4=0;...
1 - Поезд шёл 3/4 часа со скоростью 80 км/ч и 2 1/2 часа со скоростью 70...
2 - Решите уравнение (икс+37): 2*5=105 и с составлением уравнения мальчиков...
1 - Представьте данное число в виде степени какого либо числа с показателем,...
1
Преобразования Лапласа:
После преобразования получим:
Далее, для краткости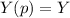
Разложим дробь на составляющие:
Условие равенства дробей:
Из первого уравнения выразим С:
Подставим в оставшиеся уравнения:
Сложим уравнения:
Находим В:
Находим С:
Разложение Y на составляющие:
Обратное преобразование Лапласа:
Искомое решение: