Решить вопрос о сходимости ряда:
ряд сходится абсолютно
ряд сходится условно
ряд расходится.

Ответы

Milki0Way0 10.10.2020 23:38

$\sum\limits_{n=1}^{\infty} a_n=\sum\limits_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n^4}$

1) Ряд знакочередующийся

2)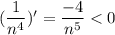 $(\dfrac{1}{n^4})'=\dfrac{-4}{n^5}$ - члены ряда убывают по модулю.

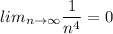
3) $lim_{n\to \infty}\dfrac{1}{n^4}=0$

Значит ряд сходится по признаку Лейбница.

Ряд из модулей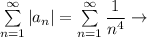 $\sum\limits_{n=1}^{\infty} |a_n|=\sum\limits_{n=1}^{\infty} \dfrac{1}{n^4}\to$ по степенному признаку.

Значит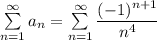 $\sum\limits_{n=1}^{\infty} a_n=\sum\limits_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n^4}$ сходится абсолютно

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

daxandra 02.03.2022 20:04

П привет всем краткое запись...

balashova1296 02.03.2022 20:02

katyadk2004 02.03.2022 20:02

Deniza23 02.03.2022 20:00

NikaAs1 02.03.2022 19:56

аринашум2007 02.03.2022 19:55

Реши уравнения, 5 72 - (х – 80 86 ) = 15 80 80...

elemesayan 02.03.2022 19:50

I need help please help you have to answer what is the measure of the missing length...

zarraban 02.03.2022 19:41

Уравнение ((4,12+?):0,1)-100=6875...

Sheik077 02.03.2022 19:40

али5553 02.03.2022 19:34

вычислить приложила фотографию...

Решить вопрос о сходимости ряда: ряд сходится абсолютноряд сходится условноряд расходится.