Решить в натуральных числах (British Mathematical Olimpiad 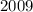 )
) 
Другие вопросы по теме Математика
Популярные вопросы
- Passive voice She thought she...(follow) by somebody. The ground......
3 - CuO → CuCl2 → Cu(OH)2 → СuSO4 → Cu Напишите уравнения реакций...
1 - Знайдіть загальний вигляд первісної для функції f(x); f(x)=x...
3 - В1. Найти циклическую частоту колебаний в контуре, емкость конденсатора...
3 - Як використовують сировину для добування етину? Відповідь потрібна...
1 - Решите математика 6-8 класс Нужно разгадать код...
3 - Рычаг под действием сил F1 = 3 Н и F2 = 9 Н находится в равновесии....
3 - Напишите, как вы понимаете цитату, взятую из романа: «…Слушайте...
1 - Мышке до норки 40 шагов.Кошке до мышки 10 прыжков.за один прыжок...
2 - Выберите правильный вариант из предложенных. 2. Nobody makes me...
3
(41;1476); (164; 1025); (369; 656); (656; 369); (1025; 164); (1476; 41)
Пошаговое объяснение:
√x+√y=√2009, x,y∈N
√y=√2009-√x
y=(√y)²=(√2009-√x)²=2009+x-2√(2009x)=2009+x-14√(41x)
y=2009+x-14√(41x)
14√(41x)=2009+x-y
14²·(41x)=(2009+x-y)²=k², k∈N⇒41x=m², m∈N
41-простое число⇒x=41a², a∈N
Аналогично доказывается, что y=41b², b∈N
√x+√y=√2009, x,y∈N
√(41a²)+√(41b²)=√2009, a,b∈N
a√41+b√41=7√41
a+b=7, a,b∈N⇒(a;b)={(1;6);(2;5);(3;4);(4;3);(5;2);(6;1)}⇒
x=41a²; y=41(14-a)², a=1;2;3;4;5;6