Решить уравнение: (за выполнение задания не более ) При каких значениях параметра a уравнение log (a+6| x|)=2 имеет ровно одно решение?

(см. объяснение)

Пошаговое объяснение:

Поскольку в условии не дано основание логарифма, то примем его равным 10. При другом его численном значении логика решения не поменяется.

Первый :

Заметим, что если x - корень уравнения, то -x тоже. Тогда единственное решение возможно, если x=0.

При этом значении переменной найдем параметр:

Покажем, что при нем у уравнения нет других корней:

(здесь ОДЗ не пишем, так как преобразованиями оно гарантируется)

Тогда такое значение параметра подходит.

Второй :

Из этой строки следует, что условие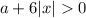 всегда выполняется.

Решим параметр в координатах (x; a):

Выполним построение:

(см. прикрепленный файл)

Откуда следует, что ответом будет .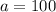

Задание выполнено!