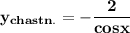Решить уравнение y'=ytgx если y(π)=2
Другие вопросы по теме Математика
Популярные вопросы
- Почему псилофиты первыми освоили сушу...
2 - Почему выход растений из воды на сушу стал возможен с появлением тканей?...
3 - В каких условиях на Земле мог осуществляться абиогенный синтез органических...
3 - Назовите основные гипотезы возникновения жизни....
1 - Каковы отличительные особенности бурых водорослей?...
3 - Какие существуют распространения плодов и семян?...
3 - Какие характерные признаки растений вы знаете?...
2 - Какие основные методы используют в биологических исследованиях?...
3 - Каковы основные особенности строения клеток растений?...
3 - В чём особенность питания одноклеточных водорослей?...
2
Дифференциальное уравнение с разделяющимися переменными
Это общее решение .
Теперь найдём частное решение.
Частное решение :