Математика: Решить уравнение с объяснением

Решить уравнение с объяснением

Ответы

cmpunk559 15.09.2020 12:45

Для начала заметим, что если x в левой стороне под корнем заменить подобным же выражением, повторяя и повторяя операцию (то есть положить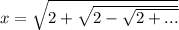 $x=\sqrt{2+\sqrt{2-\sqrt{2+...$ ), то получим верное равенство (конечно, нужно доказать, что ряд сходится, но этого сейчас не требуется, предположим, что это правда).

Получили задачу о нахождении числа $\sqrt{2+\sqrt{2-\sqrt{2+...$ ;

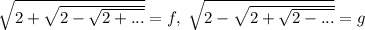Пусть $\sqrt{2+\sqrt{2-\sqrt{2+...}}}=f,\; \sqrt{2-\sqrt{2+\sqrt{2-...}}}=g$ ; Тогда получим систему: 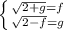$\left \{ {{\sqrt{2+g}=f} \atop {\sqrt{2-f}=g}} \right.$ ; Сделаем переход: 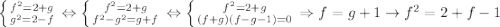$\left \{ {{f^{2}=2+g} \atop {g^{2}=2-f}} \right. \Leftrightarrow \left \{ {{f^{2}=2+g} \atop {f^{2}-g^2=g+f}} \right. \Leftrightarrow \left \{ {{f^{2}=2+g} \atop {(f+g)(f-g-1)=0}} \right. \Rightarrow f=g+1 \rightarrow f^{2}=2+f-1$ ; Осталось решить уравнение: 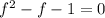$f^{2}-f-1=0$ ; Сделав отбор корней, получим: 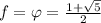$f=\varphi=\frac{1+\sqrt{5}}{2}$ ; Вспомним теперь, что 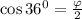$\cos36^{0}=\frac{\varphi}{2}$ , откуда и следует ответ А). Но для полноты давайте докажем этот факт.

Пусть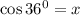 $\cos36^{0}=x$ ; Тогда 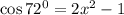$\cos72^{0}=2x^{2}-1$ ; Заметим, что 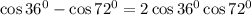$\cos36^{0}-\cos72^{0}=2\cos36^0\cos72^0$ ; Иными словами $x-2x^{2}+1=2x(2x^2-1) \Leftrightarrow (x+1)(4x^{2}-2x-1)=0$ , опять же сделав отбор корней, приходим к требуемому