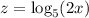Решить уравнение 7log^2_5(2x) - 20log_5(2x) - 3 = 0.
Другие вопросы по теме Математика
Популярные вопросы
- Русский язык 7 класс. Текст солнце и ветер вопрос:Выпишите из текста сочетание...
2 - А+456= d-456=c-d+a=Өтініш жауабын айтып бериниздерши керек отиниш шығарып...
2 - 105. (1) 12x = 60;112x - 15 = 13;7) 49...
2 - графики движений для двух тел изображены на рисунке 10. Напишите уравнения...
1 - Кут між радіусами проведеними до кінців хорд дорівнює 100° знайти кут між...
3 - 2. Мәтіндегі көп нүктенің орнына тиісті сөздер мен уақыт мерзімін қойып...
2 - В магазин привезли 1200 буханок хлеба до обеда продали в 3 раза меньше хлеба...
2 - В поїзді швидкість якого 54 км/год проходить відстань 600м за 30 секунд...
3 - Кейіпкерлерғе міне деме береміз.Ертенің соңында Жаманнытакка ырғаны нені...
2 - Почему старославянский язык автор книги называет рукотворным...
1
Пошаговое объяснение:
Сделаем замену переменной: