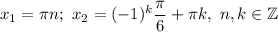Решить уравнение 1-sinx=cos2x
Другие вопросы по теме Математика
Популярные вопросы
- На двух станках отштамповали 1800 деталей за 12 ч. известно, что 180 деталей...
1 - Определите какие из данных тем требуют составления сообщения в виде 1) обобщающие...
2 - Как изменилась жизнь володи и чечевицына через 20 лет....
1 - Завершить вопросы средневековой общество нельзя считать единым на потому...
3 - Коля на 2 года старше даурена ,сауле младше коли на 3 года . возраст коли...
1 - Линия эмоций волчицы акбары 30 потому что мне нужен быстрый ответ...
1 - Написать плюсы и минусы маленькой разбойницы из произведения снежная королева...
2 - Твір з дієприслівниковими зворотами про улюблену книгу ( як я вибирала цю...
2 - Почему греки любили соревнования дайте ответ...
2 - Напишите эссе 100-120 слов на тему я хозяин нашей планеты от лица ребёнка...
1
Распишем косинус двойного аргумента:
Уравнение распадается на совокупность двух:
ответ: