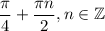Решить тригонометрическое уравнение
Другие вопросы по теме Математика
Популярные вопросы
- 1109 номер выделите целую часть числа...
1 - расстояние между поселками А и Б 40 км из поселка А выехал легковой автомобиль...
3 - Очень надо, побыстрее плз ...
3 - Қобызымқобызынқобызықобызыңыз...
1 - ФИЗИКА Двом однаковим металевим кулькам, що торкалися одна одної, передали...
3 - Сұрақтарға жауап беріңіз: · С.Торайғыров бұл өлеңде қандай мәселені көтеріп...
3 - = 2 + 2 + 2, = 2 + 3.Знайдіть площу фігури, обмеженої графіками функцій...
3 - 1. Берел қорғандарынан табылған археологиялық ескерткіштер мен тарихижәдігерлердің...
3 - У студентській групі 24 особи. Шляхом опитування з ясовано, що шестеро...
3 - 4 Отношение к труду 5 Отношение героя к окружающим людям 6 Отношение...
3
Произведение двух множителей равно нулю ⇒
левая часть уравнения принимает только положительные значения., т.е. последнее уравнение решений не имеет.
ответ: