решить тригонометрические уравнения:
а) tg x/10=1
б) tg12x=1
в) tg(3x-π/2)=1
г) tg(x-2)= -1
д) tg10x=0
Другие вопросы по теме Математика
Популярные вопросы
- описать Ивана Царевича из сказки о берендее,о сыне его Иване царевиче мне очень...
2 - Listen to the recording and choose correct option...
1 - Как нарушения природного равновесия, наблюдаемые в Казахстане, могут отразиться...
3 - Определи, какой процесс изображен на рисунке....
3 - Опишите обряд погребения саков Жетысу....
2 - Homework 1 Complete the sentences for s/he. 3aKoHunte npe noxehna ang s/he .e.g....
1 - Рассмотри фотографии.Прочитай текст. Определи его основную мысль...
2 - Ребусты шеш памагите толко дайте норманы ответ...
2 - Из кубиков объёмом 1 см³ каждый сложили прямоугольный параллелепипед. Получилось...
3 - описать Ивана Царевича из сказки о царе берендее о сыне его Ивана Царевича,...
1
1. tg(x/10)=1; x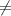 5
5 +10
+10 n
n
x/10 = /4 +
/4 +  n
n
x = 5 /2+10
/2+10 n
n
2. tg(12x)=1; x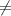
 /24 +
/24 +  n/12
n/12
12x = /4 +
/4 +  n
n
x = /48 +
/48 +  n/12
n/12
3. tg(3x- /2)=1; x
/2)=1; x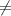
 n/3
n/3
3x- /2 =
/2 =  /4 +
/4 + n
n
3x = 3 /4 +
/4 + n
n
x = /4 +
/4 +  n/3
n/3
4. tg(x-2)=-1; x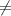
 /2+2+
/2+2+ n
n
x-2 = - /4 +
/4 +  n
n
x = - /4 + 2 +
/4 + 2 +  n
n
5. tg(10x)=0; x
 /20+
/20+ n/10
n/10
10x = n
n
x = n/10
n/10