1. Математика
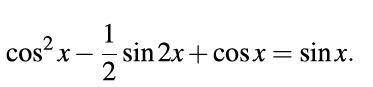
  2. решить тригонометрические уравнения.

решить тригонометрические уравнения.


решить тригонометрические уравнения.
решить тригонометрические уравнения.
решить тригонометрические уравнения.

autist1707 autist1707    1   26.07.2021 18:14    1

Ответы
NoZeX1 NoZeX1  25.08.2021 19:43

1)\ \ cos^2x-\dfrac{1}{2}\, sin2x+cosx=sinx\\\\cos^2x-\dfrac{1}{2}\cdot 2sinx\cdot cosx+cosx-sinx=0\\\\cosx\cdot (cosx-sinx)+(cosx-sinx)=0\\\\(cosx-sinx)(cosx+1)=0\\\\a)\ \ cosx-sinx=0\ |:cosx\ne 0\\\\1-tgx=0\ \ ,\ \ tgx=1\ \ ,\ \ \ x=\dfrac{\pi}{4}+\pi n\ ,\ n\in Z\\\\b)\ \ cosx=-1\ \ ,\ \ x=\pi +2\pi k\ ,\ k\in Z\\\\Otvet:\ \ x_1=\dfrac{\pi}{4}+\pi n\ ,\ n\in Z\ ,\ \ x_2=\pi +2\pi k\ ,\ \ n,k\in Z\ .

2)\ \ 2sin^2\Big(\dfrac{3\pi }{2}+x\Big)=\sqrt3\, cosx\\\\2\, cos^2x=\sqrt3\, cosx\\\\cosx\cdot (2cosx-\sqrt3)=0\\\\a)\ \ cosx=0\ \ ,\ \ \ x=\dfrac{\pi}{2}+\pi n\ ,\ n\in Z\\\\b)\ \ cosx=\dfrac{\sqrt3}{2}\ \ ,\ \ \ x=\pm \dfrac{\pi}{6}+2\pi k\ ,\ k\in Z\\\\\\Otvet:\ \ x_1=\dfrac{\pi}{2}+\pi n\ ,\ x_2=\pm \dfrac{\pi}{6}+2\pi k\ ,\ \ \ n,k\in Z\ .

\star \ \ sin\Big(\dfrac{3\pi }{2}+x\Big)=-cosx\ \ ,\ \ \ (-cosx)^2=cos^2x\ \ \star

3)\ \ cos2x-\sqrt2\, cos\Big(\dfrac{3\pi}{2}+x\Big)-1=0\\\\cos^2x-sin^2x-\sqrt2\, sinx-1=0\\\\(1-sin^2x)-sin^2x-\sqrt2\, sinx-1=0\\\\-2sin^2x-\sqrt2\, sinx=0\\\\-\sqrt2\, sinx\cdot (\sqrt2\, sinx+1)=0\\\\a)\ \ sinx=0\ \ ,\ \ x=\pi n\ ,\ n\in Z\\\\b)\ \ sinx=-\dfrac{1}{\sqrt2}\ \ ,\ \ \ sinx=-\dfrac{\sqrt2}{2}\ \ ,\ \ x=(-1)^{k}\cdot \Big(-\dfrac{\pi}{4}\Big)+\pi k\ ,\ k\in Z\ ,\\\\x=(-1)^{k+1}\cdot \dfrac{\pi }{4}+\pi k\ ,\ k\in Z

Otvet:\ \ x_1=\pi n\ ,\ \ x_2=(-1)^{k+1}\cdot \dfrac{\pi }{4}+\pi k\ ,\ \ n,k\in Z\ .

ПОКАЗАТЬ ОТВЕТЫ
dasha34presnova dasha34presnova  25.08.2021 19:43

для первого

Переносим sinx влево:

cos2x – (1/2)·2·sinx·cosx + cosx – sinx=0

Раскладываем на множители группировки:

cosx·(cosx–sinx)+(cosx–sinx)=0

(c0sx–sinx)·(cosx+1)=0

cosx–sinx=0 или cosx+1=0

tgx=1 или cosx=–1

x= (π/4)+πk, k∈Z или x= π+2πn, n∈Z

О т в е т. (π/4)+πk, π+2πn, k,n∈Z

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Гыгуль Гыгуль  07.11.2021 09:22
Площина α перетинає сторони ВА і ВС трикутника АВС у точках Н і К відповідно. Доведіть, що якщо Н і К- середини сторін АВ і ВС, то АС //α....
311020029332 311020029332  07.11.2021 09:21
решить задачу по теории вероятности, это задача из разряда задач с геометрическим определением. Ниже мое решение, у меня получается площадь фигуры по интегралу отрицательная,...
hjhjhjhhhhhhh hjhjhjhhhhhhh  07.11.2021 09:21
при делении 1 числа на другое оказалось что частное в 20 раз меньше делимого и в 21 раз больше делителя чему равно делимое, делитель и частное...
mohammadroshann mohammadroshann  07.11.2021 09:21
Отрезок длиной 50 разделен на три различные части. Найдите расстояние между серединами крайних отрезков, если длина средней части равна 22....
talanovaelena2 talanovaelena2  07.11.2021 09:19
Найдите наибольшее число-палиндром, которое делится на 99...
Вика1774574747 Вика1774574747  07.11.2021 09:17
Саша, Леша и Миша решили купить пиццу. Саша заплатил 80 рублей. Леша — половину от стоимости пиццы, а Миша смог оплатить только четвертую часть от стоимости ПИЦЦЫ. Сколько...
katya022 katya022  07.11.2021 09:17
, под a и b Желательно с подробным решением и объяснением)...
pampuzik pampuzik  07.11.2021 09:17
(Х+10) ×2=20 С решением и проверкой ❗...
2727472927у 2727472927у  07.11.2021 09:15
4 целых 1/5 умножить на 2 целых 1/7...
megastas777 megastas777  07.11.2021 09:15
Медіана CD трикутника ABC утворює зі сторонами AC і BC кути a і b відповідно BC = a. Знайдіть медіану CD....

Популярные вопросы